Decimal to Binary

Decimal to Binary Converter

With the decimal to binary converter tool, you can convert the number from base 10 to base 2 within a matter of minutes. Enter the decimal number in the input box and click on the convert button to convert it into a binary number.

_{☛ Also Check: Binary to Decimal Converter}

Decimal to Binary Conversion

Decimal to binary conversion means when we convert a number from the decimal number system to the binary number system. All number systems have a base which is determined by the total number of digits that are used in the number system. For example, the binary number system has a base of 2 since it uses only two digits to represent a number. Similarly, the decimal number system has a base of 10, because it has 10 digits to represent a number. Let us understand the decimal number system and the binary number system and then move on to the conversion of decimal to binary.

How to Convert Decimal to Binary?

Decimal to binary number can be converted by two methods:

• Converting decimal to binary number using our online free tool.
• Converting it manually.

To convert numbers from decimal to binary, the given decimal number is divided repeatedly by 2 and the remainders are noted down till we get 0 as the final quotient. The following steps is considered as the decimal to binary formula that shows the procedure of conversion.

• Step 1: Divide the given decimal number by 2 and note down the remainder.
• Step 2: Now, divide the obtained quotient by 2, and note the remainder again.
• Step 3: Repeat the above steps until you get 0 as the quotient.
• Step 4: Now, write the remainders in such a way that the last remainder is written first, followed by the rest in the reverse order.
• Step 5: This can also be understood in another way which states that the Least Significant Bit (LSB) of the binary number is at the top and the Most Significant Bit (MSB) is at the bottom. This number is the binary value of the given decimal number.

Let us understand this with an example.

Example: Convert the decimal number 13₁₀ to binary.

Solution: We will start dividing the given number (13) repeatedly by 2 until we get the quotient as 0. We will note the remainders in order.

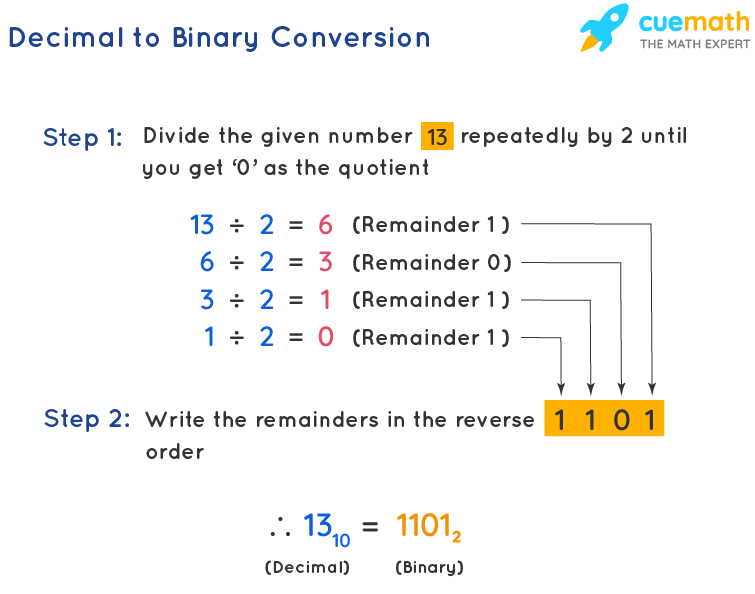
Division by 2	Quotient	Remainder
13 ÷ 2	6	1 (LSB)
6 ÷ 2	3	0
3 ÷ 2	1	1
1 ÷ 2	0	1 (MSB)

After noting the remainders, we will write them in such a way that the Most Significant Bit (MSB) of the binary number is written first, followed by the rest. Therefore, the binary equivalent for the given decimal number 1310 is 11012. This means that 1310 = 11012.

Decimal to Binary Table

Decimal Numbers	Binary Numbers
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111
16	10000
17	10001
18	10010
19	10011
20	10100