How to Convert Binary to Decimal

Binary to Decimal

Binary to decimal conversion is done to convert a number given in the binary number system to its equivalent value in the decimal number system. A number system is a format to represent numbers in a certain way.

• The binary number system is used in computers and electronic systems to represent data and it consists of only two digits which are 0 and 1.
• The decimal number system is the most commonly used number system around the world which is easily understandable to people.

Binary to decimal conversion can be done by two methods - the positional notation method and the doubling method. Let us learn how to convert binary to decimal using some binary to decimal conversion examples.

Binary to Decimal Conversion

Binary to decimal conversion is done to help read large binary numbers easily in a form that humans can understand. But how to convert binary to decimal? There are two methods to convert a number from binary to decimal number system.

• Positional Notation Method
• Doubling Method

Let us understand these binary to decimal conversion methods in detail.

Binary to Decimal Conversion Using Positional Notation Method

The positional notation method is one in which the value of a digit in a number is determined by a weight based on its position. The steps to convert binary to decimal are as follows:

• Step 1: Multiply each digit starting from the rightmost digit by the powers of 2. Here, we start with 2⁰ and increase the exponent by 1 as we move onto the left side.
• Step 2: The sum of all these values obtained for each digit gives the equivalent value of the given binary number in the decimal system.

Let us understand this with the help of examples.

Example: Convert the binary number 101101₂ to a decimal number.

Solution: Observe the following steps to understand the binary to decimal conversion. In any binary number, the rightmost digit is called the 'Least Significant Bit' (LSB) and the left-most digit is called the 'Most Significant Bit' (MSB). For a binary number with 'n' digits, the least significant bit has a weight of 2⁰ and the most significant bit has a weight of 2^n-1.

• Step 1: List out the exponents of 2 for all the digits starting from the rightmost position. The first power would be 2⁰ and as we move on to the left side it will be 2¹, 2², 2³, 2⁴, 2⁵,... In the given example, there are 6 digits, therefore, starting from the rightmost digit, the weight of each position from right to left is 2⁰, 2¹, 2², 2³, 2⁴, and 2⁵.

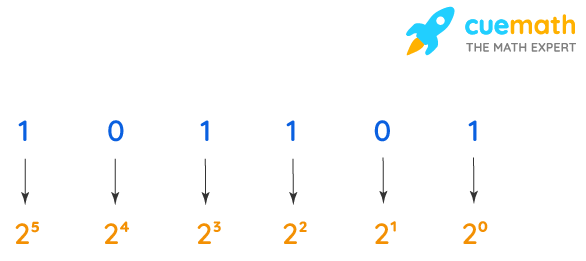
• Step 2: Now multiply each digit in the binary number starting from the right with its respective weight based on its position and evaluate the product. Observe the figure shown below to relate to the step.

• Step 3: Finally, sum up all the products obtained for all the digits in the binary number, which gives the decimal equivalent of the given bu=inary number. i.e., 101101₂ = 45₁₀

_{☛ Also Check: Binary to Decimal Calculator}

Binary to Decimal Conversion Using Doubling Method

As the name suggests, the process of doubling or multiplying by 2 is done to convert binary to decimal. This method involves the following steps to convert bin to dec. Let us use the same example for converting the binary number 101101₂ to decimal.

Example: Convert the binary number 101101₂ to decimal using doubling method.

Solution: Observe the following steps given below to understand the binary to decimal conversion using the doubling method.

• Step 1: Write the binary number and start from the left-most digit. Double the previous number and add the current digit. Since we are starting from the left-most digit and there is no previous digit to the left-most digit, we consider the double of the previous digit as 0. For example, in 101101₂, the left-most digit is '1'. The double of the previous number is 0. Therefore, we get ((0 × 2) + 1) which is 1.
• Step 2: Continue the same process for the next digit also. The second digit from the left is 0. Now, double the previous digit and add it to the current digit. Therefore, we get, [(1 × 2) + 0], which is 2.
• Step 3: Continue the same step in sequence for all the digits. The sum that is achieved in the last step is the actual decimal value. Therefore, the result of converting the binary number 101101₂ to a decimal using the doubling method is 45₁₀

Observe the figure given below to relate to the steps and understand how the doubling method works.

Binary to Decimal Conversion Formula

We use the following conversion formula to convert the binary number d_n-1...d₂d₁d₀ with n digits into decimal:

(Decimal Number)₁₀ = (d₀ × 2⁰) + (d₁ × 2¹) + (d₂ × 2² )+ ..... + d_n-1 × 2^n-1)

Let us see the application of the above binary to decimal formula and learn how to convert binary to decimal using the following example.

Example: Convert 1110₂, from binary to decimal using the binary to decimal formula.

Solution: We start doing the conversion from the rightmost digit, which is '0' here.
(Decimal Number)₁₀ = (d₀ × 2⁰) + (d₁ × 2¹) + (d₂ × 2² )+ ..... (d_n-1 × 2^n-1),
= (0 × 2⁰) + (1 × 2¹) + (1 × 2²) + (1 × 2³)

= (0 × 2⁰) + (1 × 2¹) + (1 × 2²) + (1 × 2³)

= 0 + 2 + 4 + 8

= 14

Therefore, 1110₂ = 14₁₀

Binary to Decimal Conversion Chart

The binary to decimal conversion of the first 20 decimal numbers is displayed in the chart given below.

Binary	Decimal
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
1011	11
1100	12
1101	13
1110	14
1111	15
10000	16
10001	17
10010	18
10011	19
10100	20

Binary to Decimal Conversion Example

1. Example 1: Find the decimal value of the binary number 11001011₂ using the positional notation method of binary to decimal conversion.

   Solution:

   By the positional notation of binary to decimal conversion, we multiply every digit in the binary number with its base raised to the power based on its position. This is done by starting from the rightmost digit and moving on to the left and summing up all the values.

   In the binary to decimal conversion shown below, we start from the right and move towards the left.

   11001011₂ = (1 × 2⁰)+ (1 × 2¹)+ (0 × 2²)+ (1 × 2³) + (0 × 2⁴) + (0 × 2⁵) + (1 × 2⁶) + (1 × 2⁷)

   = (1 × 1) + (1 × 2) + (0 × 4) + (1 × 8) + (0 × 16) + (0 × 32) + (1 × 64) + (1 × 128)

   = 1 + 2 + 0 + 8 + 0 + 0 + 64 +128

   = 203

   Answer: ∴ 11001011₂ = 203₁₀